Determination of the magnetostrictive length variations in FeSi electrical steels
General
The magnetostrictive length variations λ are a consequence of the magnetizing processes in ferrousmagnetic materials.
The magnetostriction value λ depends on the crystal orientation.
For the crystal lattice of the FeSi electrical steel the magnetostriction is positiv in cube edge direction [100]. When magnetizing the material becomes longer. The magnetizability is made easier by tension stresses. There are compression stresses in the material or are applied them, one needs more energy for magnetizing, the magnetization characteristic B(H) runs flatter.
In surface diagonal direction [110] the magnetostriction changes its sign.
It is positive up to high field strengths (H ≈ 40,000 A/m) and becomes then negative.
In cube diagonal direction [111] the magnetostriction is negative. With magnetization in this direction the material becomes shorter. In this case the magnetizability is facilitated by compression stresses.
When magnetizing in general very many crystallites are included. If the material does not have a preferred orientation, one can determine the function of the resulting magnetostriction by addition of the curves of these three directions for instance. If a specific orientation is more frequent than other, the magnetostriction value changes accordingly.
Measuring sensors
The magnetostrictive length variations λ = Δl/l can be determined with different sensors. Magnettechnik uses strain gauges (DMS). DMS are sensors with linear connection between relative resistance (ΔR/R0) and relative length variation (Δl/l0).
The change of resistance (ΔR/R0) is measured.
Measuring task
The functions of time t of the magnetostriction λ(t), of the flux density B(t) and of the polarization J(t) respectively should be measured.
For the measurements strain gauges DMS glued on the upper and lower surface of the samples (EPSTEIN strips 30 * 280mm²).
The results of measurements are represented in general
- as loop λ(t) over B(t) and/or J(t)
- as function λ^(B^) and/or λ^(J^)
In the case of the first mentioned representation λ(t) over B(t) and/or J(t) the well-known butterfly curves result. The course of these curves is dependent
- on the microstructure (composition, orientation distribution and/or texture)
- on internal stresses or applied tensions in the sample
- on the homogeneity of the changes of flux density (δB/δV) in the sample
- on the function of time B(t) of the flux density B in the material
In the literature the kind and quantity of the influence of these factors are reported differently frequently and intensively.
However there are rarely test results about the influence of inhomogeneous spatial (δB/δV) and nonsinusoidal (δB/δt) changes of flux density on the magnetostriction λ.
Results of measurements (examples)
It is well-known that the specific total losses P to be determined at sinusoidal function of time of the flux density B(t)~B^*sin(ωt).
A magnetizing with nonsinusoidal of B(t) is usually characterised
- by higher-frequency harmonic waves with higher eddy currents ieddy ~ uind ~ (dB/dt)
- by an inhomogenous magnetization of the sample in thickness direction (field displacement)
and lead thereby to not generally comparable loss values.
How strongly the magnetostrictive results of measurement are affected by the function of time of B(t) and/or J(t), is to be demonstrated by a comparison of two series of measurements, with those selected samples successively
- in a first coil system „Sp_1“ to Bmax ≈ 1.5T sinusoidally
- in a second coil system „Sp_2“ to Bmax ≈ 1.3T sinusoidally
were magnetized.
In the first diagram the peak to peak functions λ^(J^) of the selected specimen are represented.
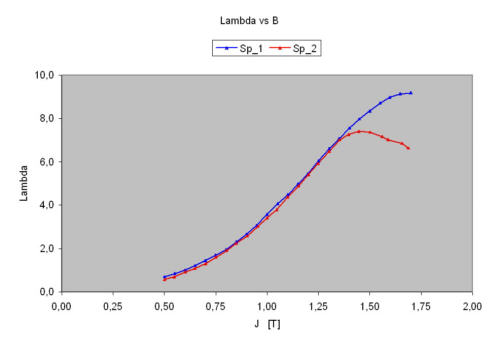
One notices that the measured values in the two coil systems
- for polarizations J <≈ 1.3T agree
- deviate for polarizations J ≈> 1.3T from each other.
In the magnetization range J ≤ 1.3T the function of time of the polarization J(t) is sinusoidal in both coil systems according to J(t) ~ J^ *sin(ωt). With the higher magnetization J of the sample in the coil system Sp_2 the function of time J(t) differs increasingly from the sine form.
In the following diagrams
- the function of time of the polarization J(t)
- the function of time of the magnetostriction λ(t)
in the two coil systems themselves represented (J^ = 1.5T).
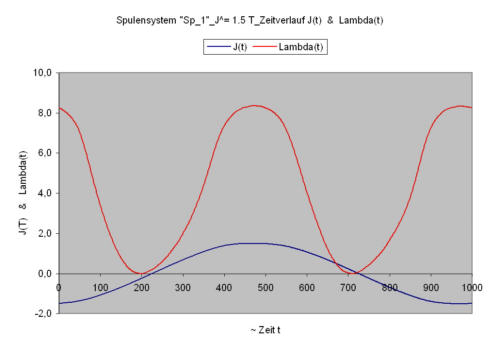
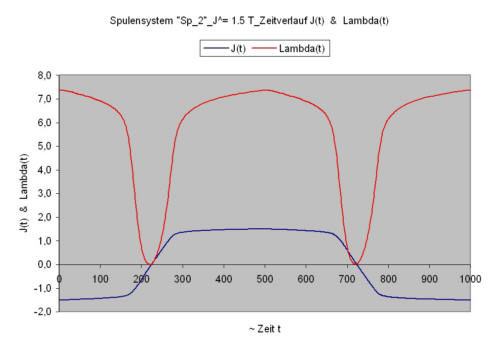
It is to be noticed that
- for the coil system „Sp_1“ J(t) ~ sin(ωt) & λ(t) ~ sin(ωt)
- for the coil system „SP_2“ J(t) ≠~ sin(ωt) & λ(t) ≠~ sin(ωt)
applies. Only in the coil system 1 the material is sinusoidally magnetized.
In the coil system 2 the magnetization of the volume occurs within in a short time interval.
The rates of change of the flux density (dB/dt) ~ uind ~ ieddy , by those
- the size and the function of time of the eddy currents i(t)
- the field displacement and inhomogeneous volume magnetization (δB/δV)
in the sample to be considerably determined, differ when both measurements are compared.
In the following diagram the λ(J)-curves for these two measurements are drawn.
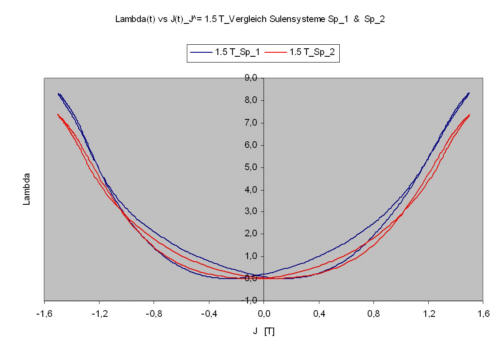
Summary
The magnetostriction of different FeSi electrical steels were determined.
In the the work the influence of the function of the time derivative (dB/dt) ~ uind ~ ieddy on the results of the magnetostriction measurements was examined in particular.
Because in technical magnetic circuits the function of time B(t) of the flux density is not sinusoidal in general, is recommended, to measure the magnetostriction under application near magnetization conditions.
By an example the influence of the function of time B(t) of the magnetic flux density on the results of dynamic magnetostriction measurements is described.
Since in technical magnetic circuits the time-function B(t) of the flux density is not sinusoidal in general, the conditions of the measurements should be adapted to the operating conditions in the technical circle to a large extent, in order be transferred the results by magnetostriction measurements and be able to use.