Magnetic Fields for Degaussing
General
Magnetic fields are described
- by the field strength H [kA/m], [Oe]
- by the flux density B = μ0 * H [T], [kG], [G].
In degaussers accessible magnetic air-fields are required, in which
- hard disc drives ( size up to 3.5”)
- magnetic tape cassettes (LTO specification , ULTRIUM format)
moved into or through.
Magnetic fields H are generated
- by air coils without core or
- by ferromagnetic yokes with air gap.
The requirements concerning the magnetic fields for erasure data follow accordingly from
- the needed magnetic field strength Hair and
- the geometric dimensions of the disks/ cassettes.
The strength of the field should be H > 800kA/m resp. B = µ0*H > 1,0T.
The geometrical dimensions of the 3.5”-hard disks are l * b * h ≈ 147mm * 102mm * 26mm.
The 3.5” magnet disks with magnetic layer have a diameter Ø = 3,5*25,4mm = 88,9mm.
Electromagnetic field excitation
The relationship between the magnetomotive force Θ = n * i and the magnetic flux Φ in a magnetic circuit is described by Θ = n * i = Φ * Rmagn.
The magnetomotive force Θ = n*I is the power source and is calculated from the number of windings of the field coil and the field current.
The magnetic resistance Rmag = Θ / Φ = lmag/μ0*μ*A depends on lmag = magnetic path length and μ = magnetic permeability.
In a magnetic circuit consisting of different magnetic materials the resistance elements are added together.
For a yoke with air gap is the expression for Θ = n*i = Φ*Rmag = Φ*(Rmag.yoke + Rmag.air).
Field excitation in an air-core coil (coil without core)
A strong magnetic field force H along a path length lmagn ≈ 30mm is prerequisite for the erasure of data.
In the HELMHOLTZ-coil (see picture) a very homogeneous field is formed in a cylindrical volume
(axial l ≈ R/3, radial r ≈ R/2) between the two single coils.
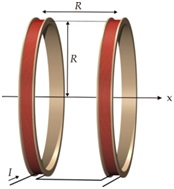
To achieve a field strength H = 800kA/m resp. a flux density B = 1.0T in an area
- with an axial length l> 25.4 mm and
- a cross section with D ≈ 3.5” ≈ 90mm
a magnetomotive force Ө ≈ 100,000 A is required.
Assuming a max. current density j = 5A/mm² results for the total cross section ACu of the Cu-winding a value ACu total ≈ 20,000 mm².
From this results the required strong magnetic fields can not be generated in air-core coils with conventional industrial currents or current densities.
The magnetic field must be generated by a current impulse from a capacitor discharge.
Because of the short-time current flow, the heat generation per evolving field is limited, despite very high current densities.
Such a solution is used in the magnetization devices for magnetization of hard magnets for some time. (www.m-pulse.eu).
Field excitation in an air gap of a yoke
FUJITSU has developed a powerful degausser with a field which is generated by rare-earth permanent magnets in the air gap of a double-E yoke.
The data medium (hard disc drives, magnetic tape cassettes) are moved through the field between the rectangular poles.
The larger side of the rectangle is larger than the diameter of a 3.5” hard drive disc.
The field in the gap of a ferromagnetic yoke can also electromagnetically generate (see sketch).
In this case the magnetic force Θ generates
- a magnetic flux Φ through the magnetic circuit according to Θ = n*i = Φ(Rmag. yoke+Rmag. gap)
- magnetic fields in the yoke and in the gap according to Θ = n*i = ΣHj * lj ≈ (Hl)yoke + (Hl)gap
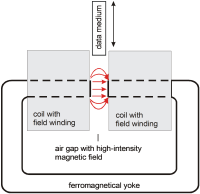
The magnetic reluctance of the air gap Rmag. gap = (l/μ0*A)gap is quantitatively difficult to determine due the widening of the field and the enlargement of the cross sectional area A (see drawing).
This spreading depends on
- the gap length
- the ratio of the gap length to the transverse dimensions of the yoke or the pole
- the excitation of the ferromagnetic yoke resp. the poles.
and involves for the magnetic field in the air gap of a yoke
- an enlargement of the cross section
- a decrease of the flux density B
- an increase of the inhomogeneity of the flux density B
The unwanted decrease of flux density B can be influenced and limited by the shaping of the poles and the optimisation of geometric dimensions of the pole.